Условия, ветвление, отладка

Представление целых чисел в памяти компьютера

Есть различные способы хранить знаковые целые числа в памяти. Один из них — sign-magnitude, то есть первый бит отведен на знак, остальные — на модуль. Это кажется более естественным, но только не для компьютера.

Например: \(-6\) в sign-magnitude будет представлено как 1110, где 1 — знак (отрицательный), а 110 — модуль (\(110_2 = 4 + 2 = 6_10\))

Бинарное значение Sign-magnitude Беззнаковое
\(00000000\) \(0\) \(0\)
\(00000001\) \(1\) \(1\)
\(\ldots\) \(\ldots\) \(\ldots\)
\(01111111\) \(127\) \(127\)
\(10000000\) \(-0\) \(128\)
\(10000001\) \(-1\) \(129\)
\(\ldots\) \(\ldots\) \(\ldots\)
\(11111111\) \(-127\) \(255\)

В sign-magnitude первый бит — знак, остальные — модуль. В беззнаковом представлении все биты — значение.

В качестве примечания стоит отметить способ, как можно легко представлять в двоичной системе степени двойки: \[2^0 = 1 = 1_2\] \[2^1 = 2 = 10_2\] \[2^2 = 4 = 100_2\] \[ 2^n = 1 \underbrace{0 \dots 0}_{n} \] \[ 2^n - 1 = 1 \underbrace{0 \dots 0}_{n} - 1 = \underbrace{1 \dots 1}_{n} \] Запомнив примеры выше, возможно моментально переводить такие числа как \(255\), \(1023\), \(2048\), \(8\) и их двоичные представления.

Возвращаемся к способам хранения целых чисел. Итак, двоично-дополнительный код — это способ представления отрицательных целых чисел в памяти компьютера. Он позволяет выполнять арифметические операции над знаковыми числами так же просто, как и над беззнаковыми.

Как получить двоично-дополнительное представление отрицательного числа:

  1. Записать абсолютное значение числа в двоичной системе, используя необходимое количество бит.
  2. Инвертировать все биты (заменить 0 на 1, а 1 на 0).
  3. Прибавить 1 к полученному числу.

Пример:
Получим представление числа \(-6\) в 4-битном двоично-дополнительном коде.

  • \(+6\) в двоичном виде: 0110
  • Инвертируем все биты: 1001
  • Прибавляем 1: 1001 + 1 = 1010

Таким образом, \(-6\) в 4-битном двоично-дополнительном коде — это 1010.

Проверка:

Бит \(1\) \(0\) \(1\) \(0\)
Значение \(-8\) \(4\) \(2\) \(1\)

\(1010 = -8 + 0 + 2 + 0 = -6\)

То есть первый бит отвечает за \(-2^{n-1}\), а остальные биты — за положительные степени двойки.

Таблица 4-битных двоично-дополнительных чисел

Биты Десятичное значение
\(0000\) \(0\)
\(0001\) \(1\)
\(0010\) \(2\)
\(\ldots\) \(\ldots\)
\(0111\) \(7\)
\(1000\) \(-8\)
\(1001\) \(-7\)
\(\ldots\) \(\ldots\)
\(1110\) \(-2\)
\(1111\) \(-1\)

Замечание:
Инвертирование и прибавление 1 — это универсальный способ получить противоположное число в двоично-дополнительном коде. Например, чтобы получить \(-n\), достаточно инвертировать все биты числа \(n\) и прибавить 1.

Двоично-дополнительный код имеет несколько преимуществ: - не требуется отдельная логика для определения знака числа; - арифметические операции (сложение, вычитание) выполняются одинаково

Рассмотрим последний пункт чуть подробнее: что будет. если многократно прибавлять 1 к некоторому знаковому 8-битному числу, начиная с \(-128\), то есть наименьшего возможного значения?

Биты Десятичное значение Комментарий
\(10000000\) \(-128\)
\(10000001\) \(-127\)
\(\ldots\) \(\ldots\)
\(11111111\) \(-1\) \(11111111_2 + 1_2 = 100000000_2\). Записываем 8 правых бит
\(00000000\) \(0\)
\(00000001\) \(1\)
\(\ldots\) \(\ldots\)
\(01111111\) \(127\)
\(10000000\) \(-128\) “Зацикливание”, то есть произошло “переполнение”, “overflow”
\(\ldots\) \(\ldots\)

Переполнение целых типов

Что же произойдет, если попытаться сохранить слишком большое значение в переменную маленького размера? Например, число \(300\) в тип unsigned char (целое, беззнаковое, 8 бит).

\(300_{10} = 100101100_2\), занимает больше, чем \(9\) бит. Запишем правые \(8\) бит в нашу переменную, тогда в ней окажется \(00101100_2 = 101100_2 = 32 + 8 + 4 = 44_{10}\). Таким образом, явно ошибка выведена не будет, программа продолжит исполнение. Можно заметить, что переполнение типа соответствует взятию остатка при делении на \(2^{\operatorname{sizeof}(T)}\) в данном случае \(2^{8 \operatorname{bit}} = 256\).

Если программа будет прибавлять по 1 к некоторой переменной целого типа, то после 254 у типа char последует 255, 0, 1, 2 и так далее, так как это число беззнаковое и \(255 = 2^8 - 1\).

Покажем эту идею на примере:

#include <iostream>

int main() {
    unsigned char c_1 = 0;
    c_1 -= 1; // происходит underflow
    std::cout << (int)c_1 << '\n'; // 255

    c_1 = 300;
    std::cout << (int)c_1 << '\n'; // 44
}

Если не использовать (int)c_1  при выводе char, то число будет воспринято как код символа и будет выведена запятая или буква латинского алфавита. Этот способ явного приведения типов пришел к C++ из языка С. Рекомендуется использовать static_cast<int>(c_1) вместо (int)c_1, так как это более явно и безопасно. В примере был использован именно C-style кастинг для краткости

Условия

Логические операции

Операции сравнения соответствуют алгебре логики, которая рассматривалась на уроках информатики:

  • отрицание – НЕ, которое инвертирует (заменяет на противоположное) логическую переменную. \(\lnot A\), !A

  • конъюнкция – И, логическое умножение, истинно только при истинности обеих входящих переменных: \(A \land B\), A && B

  • дизъюнкция – ИЛИ, логическое сложение, истинно, если истинна любая из входящих переменных: \(A \lor B\), A || B

\(A\) \(\lnot A\)
0 1
1 0
\(A\) \(B\) \(A \land B\)
0 0 0
0 1 0
1 0 0
1 1 1
\(A\) \(B\) \(A \lor B\)
0 0 0
0 1 1
1 0 1
1 1 1

Такие логические операции предстоит использовать, если мы захотим потребовать, чтобы некоторые условия должны соблюдаться одновременно (конъюнкция), “хотя бы какое-то условие” (дизъюнкция). Например, положительность числа можно записать следующим образом:

\[ \begin{gathered} A = \Big\{ \text{число является отрицательным} \Big\} = \Big\{ x < 0 \Big\} \\ B = \Big\{ \text{число не равно } 0 \Big\} = \Big\{ x \ne 0 \Big\} \\ C = \Big\{ \text{число является положительным} \Big\} = \Big\{ x > 0 \Big\} \\ \text{ }\\ \ С \equiv \lnot A \land B \\\text{ }\\ \Big\{ x > 0 \Big\} \equiv \Big\{ x \ge 0 \Big\} \land \Big\{ x \ne 0 \Big\} \end{gathered} \]

Операторы сравнения

Оператор сравнения — некоторый логический оператор, который возвращает тип bool – логическое значение

  • > (больше)

  • >= (больше или равно)

  • < (меньше)

  • <= (меньше или равно)

  • == (равно)

  • != (не равно)

Синтаксис

if (<cond>) {
    // Если условие выполняется, то программа зайдет в эту область кода
} else {
    // Иначе: то есть если условие НЕ выполняется, то программа зайдет в эту область кода
}
// исполнение программы продолжится здесь вне зависимости от условия
#include <iostream>
#include <cmath>

int main() {
    int age;
    std::cin >> age;
    if (age > 12) {
        printf("You are %d years old, so, you're too old for this cartoon\n", age);
    } else {
        printf("You are %d years old, so, you're young enough for this cartoon. Enjoy!\n", age);
    }
}

Отлично! Теперь мы умеем писать простейшие условия с введенными переменные. Если же у нас есть множество вариантов развития событий, то мы можем все их предусмотреть расширенным синтаксисом условий:

if (condition1) {
    // случай, когда condition1 истинно
} else if (condition2) {
    // случай, когда condition1 ложно, а condition2 истинно
} else if (condition3) {
    // случай, когда condition1 и condition2 ложны, а condition3 истинно
} else {
    // случай, когда condition1, condition2 и condition3 ложны
}

Это дает нам неограниченные возможности изменения логики линейной программы. Например, давайте напишем контролер билетов в кино. Пусть все настоящие билеты умеют номер, который не делится на 6 и оканчивается на четную цифру. Также нужно предусмотреть пропуск сотрудников, у которых номера билетов меньше 10, и директора кинотеатра, который обладает билетом с номером 777.

#include <iostream>

int main() {
    int age;
    std::cin >> age;
    if (age > 12) {
        printf("You are %d years old, so, you're too old for this cartoon\n", age);
    } else {
        printf("You are %d years old, so, you're young enough for this cartoon. Enter the number of your\n", age);

        int ticket_id;
        printf("Enter your ticket ID:\n", age);
        std::cin >> ticket_id;
        if (ticket_id % 6 != 0 && (ticket_id % 10) % 2 == 0) {
            printf("Enjoy the movie, customer!\n");
        } else if (ticket_id >= 0 && ticket_id < 10) {
            printf("Hi! Have a nice day at work, employee\n");
        } else if (ticket_id == 777) {
            printf("Glad to see you again, the CEO!\n");
        } else { // неверный номер билета, так как ни одно из условий не было выполнено
            printf("Invalid ticket ID! Call staff for support\n");
        }

    }
    printf("Program finished\n");

}

Как показано на примере выше, к целым числам можно применять любой оператор сравнение, но с числами с плавающей точкой все обстоит немного сложнее. Вследствие особенностей их хранения, которые были рассмотрены выше, допустимо малая неточность в интерпретации записи чисел: записанное как 3.0 может быть прочитано как 3.0000001 или 2.99999999 – такое небольшое отклонение называют пределом точности при хранении числа с плавающей точкой. При сложных и масштабных вычислениях такая ошибка может накапливаться и существенно влиять на результат, поэтому в сложных математических программах учитывают некоторую погрешность результата при вычислениях, применяют алгоритмы для уменьшения этого отклонения.

Рассмотрим корректный вариант проверки равенства переменно float некоторому значению:

#include <iostream>
#include <algorithm>

int main() {
    float number;
    std::cin >> number;

    // if (number == 3.0) {
        // INCORRECT
    // }

    if (std::abs(number - 3.0) < 0.000001) { // проверяем на равенство числу 3.0
        std::cout << "you have entered 3.0\n";
    }

    printf("Program finished\n");

}

Операторы && и || в составных условиях не будут проверять лишние условия, если таковые появятся в вашей программе. Например, как только оператор || увидит, что первый операнд истинен (true), то второй операнд проверяться не будет. Аналогично и с конъюнкцией – логическим И (&&): если первый операнд false, то второй операнд проверяться не будет, ведь итог уже ясен (см. таблицы истинности выше).

Switch-case

Если нам предстоит проверить переменную на равенству множества значений, то имеет смысл использовать особую конструкцию языка – switch. Она принимает некоторую переменную переменную на вход, а затем пытается последовательно пройтись по условию и найти точное совпадение с указанными значениями.

#include <cstdint>
#include <iostream>

int main() {
    int64_t a, b;
    char operation;
    std::cin >> a >> operation >> b;

    int64_t result = 0;
    if (operation == '+') {
        result = a + b;
    } else if (operation == '-') {
        result = a - b;
    } else if (operation == '*') {
        result = a * b;
    } else if (operation == '/' || operation == ':') {
        result = a / b;
    } else if (operation == '%') {  // остаток от деления
        result = a % b;
    }

    std::cout << result << "\n";
}

Такой не самый красивый перебор точных равенств можно заменить следующей конструкцией:

#include <cstdint>
#include <iostream>

int main() {
    int64_t a, b;
    char operation;
    std::cin >> a >> operation >> b;

    int64_t result;
    switch (operation) {
        case '+':
            result = a + b;
            break;  // если не написать этот break, программа просто пойдёт дальше в код следующего блока case
        case '-':
            result = a - b;
            break;
        case '*':
            result = a * b;
            break;
        case '/':
        case ':':
            result = a / b;
            break;
        case '%':
            result = a % b;
            break;
        default:  // здесь обрабатывается случай, когда ни один case не сработал.
            result = 0;
    }

    std::cout << result << "\n";
}

Важно помнить, что переменная, которая рассматривается в switch должна быть элементарным типом (как правило, числом), std::string уже не подойдет.

Задача о принадлежности точки некоторой области

Вспомним с уроков математики, что если у нас есть график некоторой функции \(f(x)\), то область над графиком будет множеством точек, которые удовлетворяют условию \(y \ge f(x)\). Область под графиком – \(y \le f(x)\). Строгость неравенства будет отвечать за включение самой границы (графика нашей изначальной функции) в область.

Тогда любую область мы можем задать как объединение и пересечение некоторых областей. Рассмотрим вот такую задачу:

Задача 112166 на использование условий

Как мы можем описать закрашенную область:

  • ниже \(y = \sin x\)
  • ниже \(y = 0.5\)
  • выше \(y = 0\)
  • правее \(x = 0\)
  • левее \(x = \pi\)

Напишем код для решения такой задачи:

#include <iostream>
#include <cmath>

int main() {
    float x, y;
    std::cin >> x >> y;
    if (y <= std::sin(x) && y >= 0 && y <= 0.5 && x >= 0 && x <= M_PI) {
        printf("YES\n");
    } else {
        printf("NO\n");
    }

}

Решение задачи 112166 на использование условий

Отладка программ

После написание программы вы непременно столкнетесь с набором проблем: ошибкой компиляции, отсутствием вывода, некрасивый вывод ответа в консоль и еще миллион мелочей. Такие ошибки можно без труда исправить: прочитать сообщения и предложения компилятора, поправить вывод; а вот ошибку во время выполнения программы (run time error) или ошибку в логике уже не так и легко обнаружить и исправить. Рассмотрим практические способы поиска ошибок в коде.

Разбор случаев вне программы

Зная реализованную логику, возможно придумать входные данные программе, а затем вручную проследить за поведением программы “на бумаге”. Вы понимаете, какие промежуточные значения ожидаете от программы, и при несовпадении ожиданий и значений на бумаге, вы понимаете, какую операцию или логику реализовали неверно, и можете ее исправить в коде.

Основной минус такого подхода – сложность прогона больших разветвленных программ на бумаге.

Трассировка

Идея заключается в написании дополнительного вывода в программе: так вы можете проследить, куда программа приходит при ветвлении, какие промежуточные значения имеет. Если внимательно читать вывод (или, как еще его называют – логи), то можно многое понять о программе. Это полноправный способ, который позволяет быстро получить понимание, что идет не так. Основной минус: программа продолжает выполнение с прежней скоростью, понимание ее логике вы пытаетесь восстановить по полученному выводу, что не всегда удобно или даже возможно.

Отладчик

Если специальные программы (наподобие компилятора), которые по скомпилированному исполняемому файлу с записанной дополнительной информацией могут показать вам все промежуточные переменных, остановить программу на любой строке, позволить вам пройтись вместе с вашей программой строка за строкой и проследить, что и на каком этапе идет не так.

Рассмотрим отладчик подробнее:

  • breakpoint (“точка останова”) – ваша пометка строки, на которой отладчику нужно остановиться и спросить вас о дальнейших действиях. Вы можете ставить неограниченное количество таких отметок

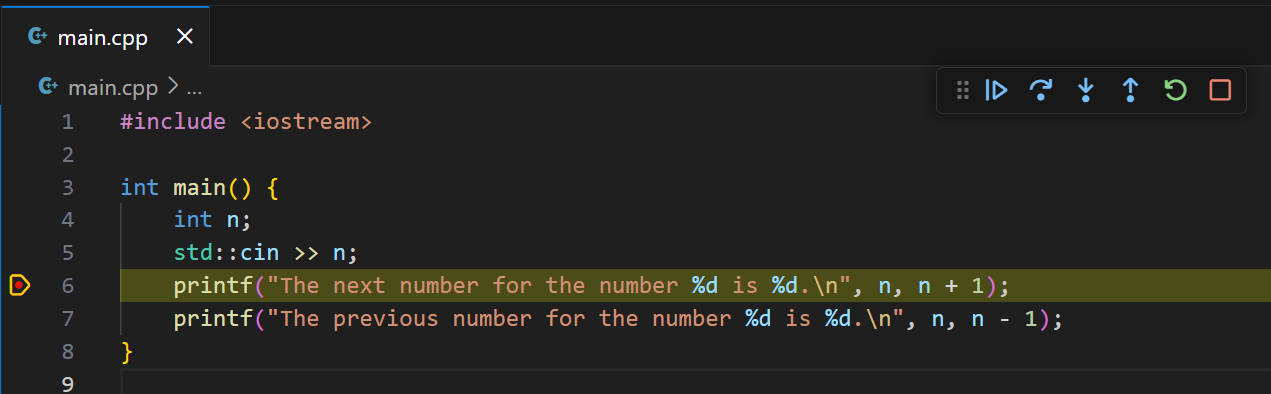Breakpoint и выделение строки при остановке Breakpoint и выделение строки при остановке

  • окно переменных – здесь можно посмотреть значения переменных на данный момент, сверить их с вашими ожиданиями в контексте задачи

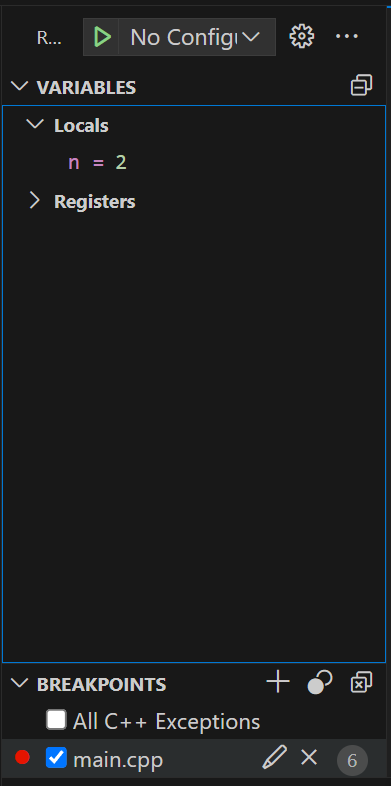    Окно с переменными Окно с переменными

  • набор команд отладчика (далее слева направо)

    • Continue – программа выйдет из режима ожидания, начнет выполнение в обыкновенном режиме до следующей точки останова (breakpoint)

    • Step over – программа перейдет на следующую строку, которая должна быть выполнена, и остановится на ней

    • Step into – если в текущей строке есть вызовы функций или неявные преобразования, то программа “провалится” в внутренние функции (будет актуально во начале второго модуля курса)

    • Step out – противоположно Step into – программа выполнит все строки до прыжка во внешнюю функцию/модуль. Поднявшись на уровень наверх, программа снова остановится

    • Restart – немедленное завершение программы, запуск сначала

    • Stop – немедленное завершение программы, выход из отладчика

Идущий далее материал не является обязательным к прочтению и не будет включен в элементы контроля

Представление чисел с плавающей точкой

Рассмотрим формат хранения чисел с плавающей точкой на примере 32-битного типа float. Для наглядность можно пользоваться калькулятором.

\(\underbrace{1 \text{ bit}}_{\text{sign}} \underbrace{8 \text{ bit}}_{\text{exp}} \underbrace{23 \text{ bit}}_{\text{mantissa}}\)

  1. sign Знаковый бит. Один, старший бит. 0 – число положительное, 1 – отрицательное.

  2. exp Показатель степени. 8-битное целое число, занимает биты с 23-го по 30-ый. Означает степень двойки, на которую будет домножаться основаная часть числа (мантисса)

  3. mantissa Дробная часть (мантисса). 23-битное целое число, содержащее значащие биты вещественного числа.

Интерпретация числа зависит от значения экспоненты:

  • Если \(0 \le exp \le 254\), то число называется нормализованным и равняется \((−1)^{sign} \times 2^{exp−127} \times \text{1.[mantissa]}\). Стоит обратить внимание на вычитание 127 из показателя, так мы получаем возможность записывать как положительные, так и отрицатльные показатели

  • Если \(exp = 0\), то число называется денормализованным и равняется \((−1)^{sign} \times 2^{−126} \times \text{0.[mantissa]}\)

  • Если \(exp = 255, mantissa =0\), то число равно \(\pm \text{inf}\)

  • Если \(exp = 255, mantissa \ne 0\), то число равно \(nan\) или \(NaN\) – not a number – “нечисло” используется для обозначения неверных операций, например, деления на 0 или извлечения арифметического корня из отрицательного числа

Интересный факт:

Вещественные числа становятся более разреженными при увеличении их модуля. Чем число ближе к нулю, тем оно ближе к ближайшему к нему другому представимому числу. А точнее, денормализованные числа идут через одинаковый шаг. Нормализованные числа с \(exp = 1\) идут через удвоенный шаг, с \(exp = 2\) – через учетверённый, и так далее. Иллюстрация распределения чисел:

Распределение чисел с плавающей точкой

Наименьшее нормализованное число: \(2^{-126} \cdot 1.0\). Наибольшего денормализованное число: \(2^{-126} \cdot 0.111111...\) Таким образом, наименьшее нормализованное больше наибольшего денормализованного числа.

Тип double хранится аналогично, но занимает 64 бита: 1 на знак, 11 на экспоненту, 52 на мантиссу.

Вопросы в качестве упражнения (приходите обсуждать ответы до/после пары, если будет время и желание): - почему нельзя точно записать любое рациональное число в памяти компьютера? - как точность записи рационального числа зависит от его модуля? при чем здесь экспонента (exp) при записи в память? - сколько есть способов записать 0? - как перемножить 2 float? то есть как манипулировать какими частями битовой записи, чтобы это было эффективно?